Чи можна передбачити майбутнє за допомогою законів фізики?
- Ігор Сальниченко
- 4 жовт. 2024 р.
- Читати 9 хв
Оновлено: 17 лист. 2024 р.
Майбутнє, здавалося б, можна передбачити за допомогою законів фізики, якщо розглядати класичну механіку. Закони Ньютона дозволяють точно прогнозувати рух об'єктів, ґрунтуючись на їхньому початковому стані. Однак із розвитком науки ми дізналися, що не все так просто. Сучасні теорії, такі як квантова механіка та теорія хаосу, значно ускладнили картину передбачення майбутнього, вводячи елементи випадковості та невизначеності.
Теорія хаосу виявила, що навіть у класичних системах малесенькі зміни в початкових умовах можуть призводити до значних наслідків, що робить довгострокове прогнозування майже неможливим. Водночас квантова механіка, з її принципом невизначеності Гайзенберга, ставить під сумнів можливість точного прогнозу в мікросвіті. Це викликає фундаментальне питання: чи можемо ми насправді передбачити майбутнє на основі фізичних законів, і які обмеження накладають сучасні наукові теорії на такі передбачення?
Детермінізм у класичній механіці
Детермінізм у класичній механіці базується на ідеї, що всі події в природі можуть бути точно передбачені, якщо відомі початкові умови системи. В основі цього лежать закони Ньютона, особливо другий закон динаміки: F=ma (де F — сила, m — маса, а a — прискорення). Цей закон описує, як зміна руху об'єкта залежить від прикладеної сили, і дозволяє будувати прогнози щодо його подальшого стану.
У класичній фізиці передбачається, що світ працює як механізм годинника, де кожен рух чи подія обумовлені попередніми станами системи. Якщо ми знаємо положення, швидкість і всі сили, що діють на об'єкт у певний момент часу, ми можемо точно розрахувати, де він буде через будь-який проміжок часу. Це і є основа класичного детермінізму.
Приклад 1: Прогнозування руху планет
Одним із класичних прикладів детермінізму є передбачення руху планет у Сонячній системі. Завдяки законам Ньютона та теорії гравітації ми можемо розрахувати орбіти планет на десятиліття чи навіть століття вперед. Для цього використовують закон всесвітнього тяжіння Ньютона:
Ця формула дозволяє астрономам обчислювати рух планет, їхні орбіти, взаємодії із Сонцем і між собою. Наприклад, за допомогою цих законів астрономи можуть передбачити точні дати та місця майбутніх сонячних і місячних затемнень, які повторюються через певний період.

Приклад 2: Вільне падіння тіл
Ще одним яскравим прикладом детермінізму є рух тіл під дією сили тяжіння. Якщо кинути об'єкт з певної висоти, то знаючи його початкову швидкість, висоту і прискорення вільного падіння (g≈9.8 м/с2), можна точно розрахувати, коли і з якою швидкістю він досягне землі. Формула для такого руху виглядає наступним чином:
Обмеження класичного детермінізму
Хоча детермінізм класичної механіки дозволяє робити точні прогнози в багатьох ситуаціях, він має свої обмеження. По-перше, він працює лише для макроскопічних об'єктів, де квантові ефекти можуть бути знехтувані. По-друге, в реальних системах часто є численні фактори, які важко або неможливо точно виміряти, такі як тертя, атмосферні умови або невідомі взаємодії, що можуть вплинути на точність передбачень. У таких випадках теорія хаосу або квантова механіка відіграють важливу роль, додаючи елементи випадковості та обмежуючи передбачуваність.
Отже, детермінізм у класичній механіці дає надзвичайно точні прогнози в ідеалізованих умовах, проте у складних системах, особливо в умовах хаотичної поведінки чи на квантовому рівні, виникають серйозні обмеження, які порушують абсолютну передбачуваність.
Теорія хаосу: межі передбачуваності
Теорія хаосу показала, що навіть у системах, які підпорядковуються детерміністським законам класичної механіки, можуть існувати серйозні межі передбачуваності. Основна ідея теорії хаосу полягає в тому, що невеликі зміни в початкових умовах системи можуть спричинити радикальні зміни в її майбутньому стані. Це явище називають чутливістю до початкових умов, що є характерною рисою хаотичних систем.
Основи теорії хаосу
Теорія хаосу виникла на межі класичної фізики та нелінійної динаміки. Вона показала, що не всі системи можуть бути точно передбачуваними, навіть якщо вони детерміновані законами природи. Іншими словами, хоча рух системи описується детерміністськими рівняннями, малі зміни в її початкових умовах можуть призводити до непередбачуваних наслідків у майбутньому.
Прикладом такого явища є класична модель маятника або подвійного маятника. У простому маятнику ми можемо точно передбачити його рух на основі законів Ньютона. Але в складнішій системі, як-от подвійний маятник, навіть невелике збурення початкових умов робить прогноз дуже складним і нестійким. Така поведінка називається хаотичною.
Ефект метелика
Один із найбільш відомих і наочних прикладів хаотичної поведінки — це ефект метелика. Ця концепція була популяризована математиком та метеорологом Едвардом Лоренцем у 1960-х роках. В ході його досліджень атмосферної динаміки, Лоренц виявив, що незначні зміни в початкових умовах моделі погоди можуть призвести до величезних змін у довгостроковому прогнозі. Він висловив це таким чином: "помах крил метелика в одному місці може викликати ураган на іншому кінці світу через деякий час".

Лоренц створив спрощену модель атмосфери (систему нелінійних рівнянь), яка показала, що точність довгострокового прогнозування погоди обмежена через чутливість до початкових умов. Це означає, що для прогнозу на тривалий час потрібні ідеально точні початкові дані, але в реальних умовах це неможливо через обмеження вимірювальних приладів і невідомі зовнішні фактори.
Прогнозування погоди та інші приклади хаосу
Прогнозування погоди є класичним прикладом застосування теорії хаосу. Модель Лоренца показала, що тривалість точного прогнозу погоди обмежена кількома днями, після чого непередбачуваність різко зростає. Це пояснюється саме ефектом метелика та хаотичною природою атмосферних процесів. Відносно малі помилки у вимірюванні температури або тиску можуть спричинити значні зміни у прогнозі через кілька днів.
Окрім атмосфери, приклади хаотичної поведінки можна знайти у багатьох інших фізичних системах: від руху рідин до поведінки зоряних систем і навіть у біології. Наприклад, у фізиці плазми чи моделюванні зірок можна спостерігати складну, хаотичну поведінку, яка робить довгострокове прогнозування дуже складним.
Математичне моделювання хаотичних систем
Основний інструмент для вивчення хаосу — це нелінійні диференціальні рівняння. Багато фізичних процесів не можуть бути описані простими лінійними рівняннями через їхню складну взаємодію різних елементів. Хаотичні системи часто описуються рівняннями, що мають нелінійний характер, тобто ті, де зміна одного параметра не призводить до пропорційної зміни іншого. Це створює складні взаємозалежності між параметрами системи, що й призводить до хаосу.
Зазвичай математичне моделювання таких систем вимагає використання комп'ютерів для чисельного розв'язання рівнянь, оскільки аналітичні рішення для нелінійних систем часто неможливі.
Обмеження передбачуваності в хаотичних системах
Хоча детермінізм є основою класичної фізики, теорія хаосу показує, що передбачуваність має свої обмеження навіть у детерміністичних системах. Найголовнішим фактором, який обмежує можливість точного прогнозування, є чутливість до початкових умов. Для точного передбачення майбутнього необхідно знати початковий стан системи з ідеальною точністю, що в більшості реальних ситуацій неможливо через технічні обмеження або недосконалість моделей.
Таким чином, теорія хаосу кидає виклик класичному детермінізму, показуючи, що не всі системи можуть бути передбачуваними в довгостроковій перспективі. Навіть якщо ми маємо детерміністичні закони, поведінка складних систем може бути хаотичною і майже непередбачуваною на практиці.
Квантова механіка: принцип невизначеності Гайзенберга
Принцип невизначеності Гайзенберга є фундаментальним елементом квантової механіки і відіграє ключову роль у розумінні того, чому в мікросвіті передбачуваність має свої обмеження. Принцип, запропонований німецьким фізиком Вернером Гайзенбергом у 1927 році, стверджує, що неможливо одночасно точно виміряти положення (x) і імпульс (p) квантової частинки. Це математично виражається через нерівність:
Ця формула показує, що чим точніше ми вимірюємо положення частинки, тим більша невизначеність в її імпульсі, і навпаки.

Природа квантової невизначеності
У класичній фізиці вважалося, що точні вимірювання всіх параметрів системи дозволяють передбачити її майбутнє. Однак квантова механіка підриває це припущення. Принцип невизначеності не є результатом недосконалості приладів вимірювання; це фундаментальна властивість природи на квантовому рівні. Квантові об'єкти, такі як електрони або фотони, не можуть мати чітко визначене положення і імпульс одночасно.
Ця невизначеність виникає через те, що частинки у квантовій механіці мають хвильову природу. Електрон, наприклад, описується хвильовою функцією, яка дає ймовірність його перебування в певній точці простору, а не точну координату, як це було б у класичній фізиці. Тому замість того, щоб говорити про точне місце знаходження частинки, квантова механіка говорить про ймовірності її виявлення в певному діапазоні координат або імпульсів.
Вплив на передбачуваність у квантовій механіці
Принцип невизначеності Гайзенберга має серйозні наслідки для передбачуваності квантових систем. У класичній механіці, знаючи точні початкові умови (положення, швидкість), можна прогнозувати майбутній стан системи з довільною точністю. Однак у квантовій механіці це неможливо, оскільки точні початкові умови не можуть бути відомі. Натомість фізики оперують ймовірнісними прогнозами.
Наприклад, при описі руху електрона в атомі, неможливо точно сказати, де він знаходиться в даний момент часу. Замість цього можна лише визначити ймовірність того, що він буде в певній точці простору. Це фундаментальне обмеження впливає на нашу здатність передбачати майбутні стани квантових систем.
Ймовірність у квантовій фізиці
Один із основних постулатів квантової механіки — це те, що стан частинки описується не чіткими числами, як у класичній механіці, а хвильовою функцією, яка містить інформацію про ймовірності. Наприклад, якщо розглядати електрон у атомі, хвильова функція дає інформацію про те, з якою ймовірністю можна знайти електрон у певному місці простору.
Замість передбачень точного майбутнього стану частинки, квантова механіка дозволяє передбачити лише спектр можливих результатів з певними ймовірностями. Це принципово відрізняється від класичного детермінізму, де майбутнє однозначно визначається початковими умовами.
Підрив класичних уявлень про передбачуваність
Принцип невизначеності Гайзенберга підриває класичне уявлення про передбачуваність і детермінізм. У класичній механіці всесвіт можна уявити як гігантський механізм, де кожна подія є результатом попередніх подій і може бути передбачена, знаючи початкові умови. Однак у квантовій фізиці такого точного детермінізму не існує.
Квантова механіка підкреслює, що природа на фундаментальному рівні є ймовірнісною. Це означає, що на рівні атомів і субатомних частинок передбачити точний результат експерименту неможливо. Можна лише говорити про ймовірність того чи іншого результату. Це не означає, що світ є хаотичним, але це вказує на те, що наше розуміння і передбачення майбутнього на квантовому рівні завжди буде обмежене.
Наслідки для фізики та технологій
Принцип невизначеності Гайзенберга має не лише теоретичне, але й практичне значення. Він накладає обмеження на точність вимірювань, які можна досягти у квантових експериментах, що є важливим для таких технологій, як квантова криптографія або квантові комп'ютери. Наприклад, у квантових комп'ютерах процес обчислень відбувається завдяки маніпуляціям квантовими станами частинок, і ймовірнісна природа цих станів відкриває нові можливості для обчислювальних процесів, яких не можуть досягти класичні комп'ютери.
Таким чином, квантова механіка та принцип невизначеності Гайзенберга демонструють, що на фундаментальному рівні природа не є повністю детермінованою. Це кардинально змінює наше розуміння передбачуваності у фізиці і ставить нові виклики для наукових досліджень у сфері квантових технологій та фундаментальних фізичних теорій.
Передбачення майбутнього на макрорівні: можливості та обмеження
Передбачення майбутнього на макрорівні є однією з найважливіших задач сучасної науки. Якщо в мікросвіті квантова механіка і принцип невизначеності Гайзенберга вносять елемент випадковості та обмежують точність прогнозів, то на макрорівні — у масштабах планет, зірок або галактик — інші фактори, такі як складність систем та нелінійні взаємодії, також значно ускладнюють прогнозування. Для розуміння цих меж передбачуваності важливо враховувати як закони квантової механіки, так і результати теорії хаосу.
Космологія та еволюція Всесвіту
У сфері космології макрорівневі передбачення мають ключове значення. Закони загальної теорії відносності Айнштайна надають інструменти для розуміння еволюції Всесвіту в дуже великих масштабах. Наприклад, на основі спостережень за червоним зсувом галактик та фонового мікрохвильового випромінювання космологи можуть передбачати розширення Всесвіту і його майбутнє.
Однак навіть у цьому масштабі існують обмеження передбачуваності. На ранніх стадіях еволюції Всесвіту домінували квантові процеси, які вплинули на формування великомасштабних структур, таких як галактики та скупчення галактик. Ці початкові квантові флуктуації були малими, але в результаті гравітаційної взаємодії вони привели до утворення всіх структур у Всесвіті. Такий взаємозв'язок між квантовими процесами і великими структурами вказує на те, що непередбачуваність у мікросвіті може мати наслідки для прогнозів у макросвіті.

Дослідження темної матерії та темної енергії також ускладнюють прогнозування майбутнього Всесвіту. Хоча загальна теорія відносності добре описує взаємодію гравітаційних сил, роль темної матерії та енергії залишається маловивченою. Це створює невизначеність у прогнозах щодо довгострокової еволюції Всесвіту, зокрема його потенційного кінця (теплова смерть, Великий розрив або інші сценарії).
Прогнозування клімату: можливості та обмеження
Прогнозування кліматичних змін на Землі є ще однією важливою задачею для науки, де зіткнення між класичними детерміністичними підходами та елементами теорії хаосу особливо помітне. Атмосферні процеси на нашій планеті є типовим прикладом нелінійних систем, що робить довгострокові прогнози складними. Теорія хаосу свідчить, що навіть невеликі зміни в початкових умовах (наприклад, температура океанів чи вологість повітря) можуть призвести до значних змін у кліматичних процесах через деякий час.
Поточні кліматичні моделі базуються на складних чисельних розрахунках, які намагаються врахувати всі ці фактори. Однак через чутливість до початкових умов точність цих прогнозів зменшується з часом. Хоча короткострокові прогнози є досить точними, довгострокові прогнози змін клімату, особливо на десятиліття або століття вперед, стають дедалі менш визначеними.
Окрім цього, квантові ефекти в атмосферних процесах не відіграють помітної ролі, але через складність взаємодії між різними шарами атмосфери, океанів та суші, довгострокові кліматичні прогнози також обмежені.
Використання квантових комп'ютерів для вдосконалення передбачень
Останні досягнення в сфері квантових технологій відкривають нові можливості для вдосконалення прогнозування на макрорівні. Квантові комп'ютери мають потенціал значно збільшити обчислювальну потужність, що дозволить створювати більш точні моделі складних систем. Завдяки здатності працювати з квантовими суперпозиціями та паралельними обчисленнями, квантові комп'ютери можуть обробляти набагато більші масиви даних, ніж класичні комп'ютери.
У майбутньому квантові комп'ютери можуть стати корисними для прогнозування таких систем, як еволюція Всесвіту або кліматичні зміни. Наприклад, вони можуть значно підвищити точність симуляцій складних атмосферних процесів або моделювання взаємодії гравітаційних та квантових ефектів на масштабах галактик. Проте, квантові технології самі по собі не усунуть фундаментальних обмежень передбачуваності, викликаних принципом невизначеності та чутливістю до початкових умов у хаотичних системах.

Передбачення майбутнього на макрорівні можливе, але має свої суттєві обмеження. Хоча класичні закони фізики дозволяють робити точні прогнози в певних умовах, теорія хаосу та квантова механіка вказують на те, що абсолютна передбачуваність є неможливою як на мікро-, так і на макрорівнях. Взаємодія між квантовими флуктуаціями, хаотичними явищами і великими масштабами Всесвіту створює складну систему, де навіть найсучасніші технології не зможуть забезпечити ідеальну точність прогнозів.
Тим не менш, розвиток квантових комп'ютерів та вдосконалення чисельних методів моделювання надають нові інструменти для поліпшення передбачень, що дозволить нам краще розуміти та прогнозувати поведінку складних макросистем, таких як кліматичні процеси чи еволюція Всесвіту.
Висновок
Фізика надає нам потужні інструменти для передбачення майбутнього на різних рівнях — від класичних систем до квантових процесів. Класична механіка дозволяє з високою точністю прогнозувати поведінку систем, які підкоряються законам Ньютона. Однак у складних системах, таких як клімат або космологічні процеси, виникають обмеження, зумовлені теорією хаосу. Маленькі зміни в початкових умовах можуть призвести до значних відмінностей у майбутніх станах, що робить довгострокові прогнози в таких системах менш точними.
Квантова механіка, зі своїм принципом невизначеності Гайзенберга, додає ще більше обмежень на передбачення у мікросвіті, де детермінізм класичної фізики більше не працює. Проте ймовірнісні підходи дають можливість прогнозувати діапазони можливих результатів.
Перспективи розвитку квантових комп'ютерів і вдосконалення методів моделювання обіцяють значні досягнення у сфері прогнозування складних систем. Хоча абсолютна передбачуваність є недосяжною, ці технології допоможуть покращити розуміння та прогнозування як макро-, так і мікросвітів.




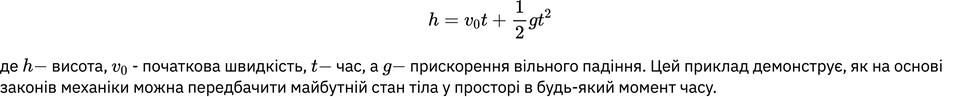

Comments